湖南省考,巧用公式秒解数量关系容斥难题!
今天,湖南公务员考试网小编为大家分享的是行测数量关系模块的经典题型——容斥问题,帮助大家学会题型的判断和对应套路的使用,赶紧一起学起来~
容斥问题
容斥问题的本质是去除重复,而解题方法是公式法和图示法。首先优先使用公式法,两集合类容斥问题的公式为:总情况数-两个条件都不满足的个数=满足条件1的个数+满足条件2的个数-两个条件都满足的个数,能够直接套用公式的题目优先套用公式。当题目中出现“只”满足一个条件这样的字眼,由于公式当中无法直接求出,可使用图示法进行求解。
那么下面我们一起看几个例题,应用一下两集合类容斥问题的两种解题方法。

【解析】
第一步,本题考查容斥问题。
第二步,能够进入工作组的员工即为两个条件都满足的人,设能够进入工作组的员工有x人,根据两集合容斥公式:总数-都不=A+B-AB,代入数据可得80-10=40+46-x,解得x=16人。因此,选择A选项。

【解析】
第一步,本题考查容斥问题。
第二步,设两门课程都没有得满分的有x人,根据二者容斥公式可得:62+34-11+x=100,解得x=15,即两门课程都没有得满分的有15人。因此,选择B选项

【解析】
第一步,本题考查容斥问题,属于二集合容斥类,用公式法解题。
第二步,共两个兴趣小组,其中80%的学生参加地理兴趣小组、50%的学生参加生物兴趣小组,根据两集合容斥原理公式:满足条件1的个数+满足条件2的个数-两者都满足的个数=总个数-两者都不满足的个数,设同时参加两个兴趣小组的学生占比为x,则有80%+50%-x=100%-0,解得x=30%,那么同时参加两个兴趣小组的共有300×30%=90(人)。因此,选择C选项。

【解析】
第一步,本题考查容斥问题。
第二步,如下图:
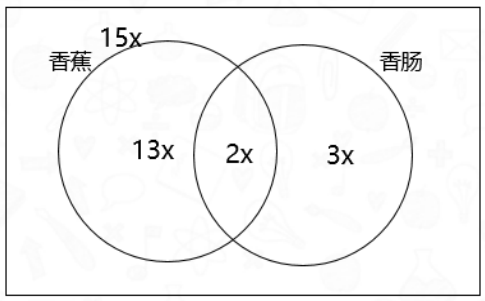
设两种食物都吃的狒狒有2x只,则只吃香肠的有3x只,根据吃香蕉是吃香肠的3倍,可得吃香蕉的有(2x+3x)×3=15x只,进食的狒狒共15x+3x=18x只,占总数的90%,共计18x÷90%=20x只狒狒,未进食的有2x只,是只吃香蕉的2/13。
因此,选择C选项。



婵犫偓閺嵮冪闁活亙娴囬埀顒€鍟ㄩ埀顑挎缁ㄣ劍绋夊顒€绀嬪ù锝呯Х閳ь剙鍟抽惁顖涚閵堝棛銈︾紓鍥ュ€曠槐鎴﹀绩閸欍儴鍘柨娑樼灱閸嬶綁宕欐繝姘嚑闁圭尨鎷�闁靛棴鎷�2025闁稿浚鍓欐慨鐔煎川濡警妯嬮柣顏冩祰娴犲牓鎳撻崘顭戞У闁兼澘鍟ㄩ埀顒婃嫹闁告梻濮撮崣鍡欑礃閵堝牅鍠婇柨娑樿嫰瑜板弶绂嶉銏犵秬闁稿繐绉烽崹鍌炴嚀娴e摜鐟�1閻庣鎷�1閻熸瑱绲块悺鐔煎嫉瀹ュ懎顫ら柨娑樿嫰閸樸倗鎷硅ぐ鎺濇殭闁告瑦鐗楃粻褰掑础濡ゅ啯闃滈柤鏉垮暞鑶╅柟椋庡枎瀹撳酣鏁嶇仦鑺ョ闊洤妫涙晶妤冩嫚閺囥埄鏆柛妤€鍤栫槐婵嬪礂閵娿儺娈扮紒妤佹閻︻垶妫冮姀锝囨Ц闁轰礁顕幃濠勬導閸曨剚鐏愰柨娑虫嫹
点击分享此信息:
 相关文章
相关文章



